 |
|
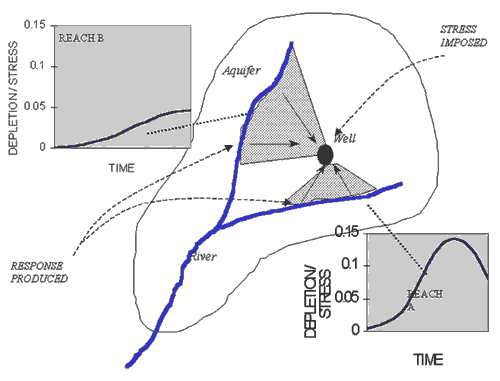
Figure
1. Concept of Stream Capture Response Functions.
|
|
Gary
S. Johnson and Donna M. Cosgrove
University of Idaho, Idaho Water Resources Research Institute Idaho Falls, Idaho and Joe Spinazola U.S. Bureau of Reclamation, Boise, ID |
PRESENTED
AT: MODFLOW '98, GOLDEN, CO., OCTOBER 4-8, 1998, SPONSORED BY THE INTERNATIONAL GROUND WATER MODELING CENTER AND COLORADO SCHOOL OF MINES. |
ABSTRACT
Numerical models, such
as MODFLOW, provide excellent tools to assist in the water resourc decision
making process. A simplified representation of the system may, in some cases,
be obtained by the development of response functions from numerical models.
These functions express temporal relationships between cause and effect at specific
points within the aquifer and are developed through simulation. The functions
are valid so long as the equations governing flow in the system are approximately
linear with respect to aquifer head.
. Response functions can be generated from multiple MODFLOW simulations or more simply from the MODFLOW based MODRSP program. Response functions can be developed to describe how aquifer water levels, aquifer storage, surface water depletion, or ground water flow velocities are affected by ground water pumping or recharge in any prescribed location. In areas where the use of response functions is valid, they can provide a highly useful tool for water managers.
INTRODUCTION
Numerical models such as
MODFLOW can produce predictive simulations of cause and effect when properly
calibrated and applied to an area. This process normally involves comparing
results of a series of predictive scenarios to results of a base study, possibly
projecting current conditions into the future. The process is valid and useful;
however, it requires at least one simulation and comparison for each scenario
of interest and has limited capability in presenting cause and effect relationships
in more general terms.
Response functions are analytical expressions, graphs, or coefficients that describe the relative response of the aquifer system at a given location to a unit stress at a second location (figure 1, below). Because the response is expressed in relative terms, it may be scaled to any magnitude of stress desired. The functions may express transient or steady-state response of the system to the stress. The development and use of response functions require that response is proportional to the magnitude of the stress; consequently, the governing equations must be approximately linear. Responses may be in terms of aquifer water level change (drawdown), changes in head-dependent flux (capture), change in storage, or changes in ground-water flow velocity. Similar or identical concepts have been called discrete kernels (Morel-Seytoux and Daly, 1975), influence coefficients (Illangasekare and Morel-Seytoux, 1982), algebraic technologic functions (Maddock, 1972) and "drawdown simulations" (Anderson and Woessner, 1992). The assumption of linearity of the governing equations is the major constraint of the application of response functions and will be addressed in greater detail in the following section.
 |
|
Figure
1. Concept of Stream Capture Response Functions.
|
Response functions can aid in visualization and conceptualization of pumping and recharge effects because the response is assumed to be proportional to the stress. This relationship allows a generic presentation of cause and effect relationships. Hubbell, et al (1997) used a similar approach to describe zones in the Snake River Plain aquifer where ground-water pumping predominantly affects one of four reaches of the Snake River. Refinement of the zones developed by Hubbell, et al (1997) may ultimately form the basis for conjunctive administration of water rights in the eastern Snake River Plain.
Quantification of impacts from individual pumping or recharge activities may be required in adjudication of water rights or development of mitigation plans. Johnson et al (1993) evaluated the depletion of springs from the Snake River Plain aquifer by generating response functions for 18 selected stress locations on the eastern Snake River Plain. The impacts of ground-water use on spring discharge and flow of the Snake River can be approximately assessed for any location on the Plain by using response functions from the nearest location. Similar information may ultimately be used to establish mitigation requirements for ground water pumpers.
The simplified linear form of the response functions permits incorporation into surface water models and optimization schemes. El-Beshri and Labadie (1994) incorporated capture response functions into the surface water model MODSIM (Labadie, 1991). Response or influence coefficients have been applied in simulation/optimization models by several researchers including Ejaz and Peralta (1995).
Response functions can be generated analytically or from calibrated numerical models. Analytically generated response functions are little more than calibration of an analytic expression, such as the Theis Equation, to conditions representing a specific aquifer. Substituting appropriate values for aquifer transmissivity and distance (representing a specific stress location and response location) graphs, response coefficients, or equations can be developed to show how drawdown or stream depletion from a unit stress is related to time. The numerous assumptions inherent in analytical techniques can be avoided by generating response functions from numerical models. The numerical model can be either 1) run under a special set of conditions to evaluate response to a unit stress, or 2) if MODFLOW is used, a special adaptation, MODRSP (Maddock and Lacher, 1991), can be used to generate the response relationships.
The purpose of this paper is to describe how response functions may be generated either directly from a MODFLOW simulation, or through application of MODRSP.
CONSTRAINTS
ON USE OF RESPONSE FUNCTIONS
Response functions describe
the relative response of the aquifer or stream to an applied aquifer stress.
It is normally necessary to assume that the responses of multiple stresses may
be superimposed in order to describe aquifer response in general terms. The
use of response functions is therefore normally limited to cases where the system
can be adequately described using linear equations Reilly, et al (1987) describe
the use of linear equations in ground water flow systems.
Numerical models, including MODFLOW, may be based on governing equations that are either linear or non-linear. The partial differential equation representing ground-water flow is linear with respect to the independent variable representing aquifer head. This equation is the foundation from which the finite-difference expressions for saturated, confined, ground-water flow are developed. The linearity of the equation implies that superposition concepts, including response functions, are valid when this equation describes flow within a system.
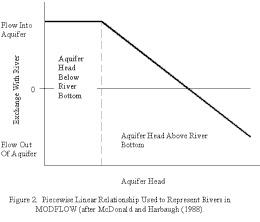 MODFLOW
and other numerical model codes include other head-dependent relationships representing
system boundaries. Head-dependent functions exist to represent aquifer exchange
with rivers, drains, evapotranspiration, and other features. Many of these are
represented as piece-wise linear relationships (figure 2). The discontinuity
in the linearity of these relationships cannot be accommodated in the use of
response functions. The functions will be valid so long as conditions within
the aquifer do not cross the discontinuity of slope. When simulating rivers
using the River or Streamflow Routing Packages, this is equivalent to requiring
that the aquifer heads either continuously remain above or below the elevation
of the bottom of the river. The river cannot transition from head-dependent
to perched conditions. When simulating drains, the aquifer head at the drain
cannot transition across the elevation of the drain. The drain must either remain
active or inactive.
MODFLOW
and other numerical model codes include other head-dependent relationships representing
system boundaries. Head-dependent functions exist to represent aquifer exchange
with rivers, drains, evapotranspiration, and other features. Many of these are
represented as piece-wise linear relationships (figure 2). The discontinuity
in the linearity of these relationships cannot be accommodated in the use of
response functions. The functions will be valid so long as conditions within
the aquifer do not cross the discontinuity of slope. When simulating rivers
using the River or Streamflow Routing Packages, this is equivalent to requiring
that the aquifer heads either continuously remain above or below the elevation
of the bottom of the river. The river cannot transition from head-dependent
to perched conditions. When simulating drains, the aquifer head at the drain
cannot transition across the elevation of the drain. The drain must either remain
active or inactive.
Unconfined aquifers require a different form of the partial differential representing ground water flow. The Boussinesq equation is not linear with respect to aquifer head. Superposition and response functions cannot, therefore, be used unless the Dupuit assumption (small head change relative to aquifer thickness) can be applied. If this is not the case, then the response of the system is significantly dependent on other stresses occurring simultaneously, and the system response cannot be expressed without describing all concurrent recharge and discharge activities. Response functions cannot be used in this case.
There are many cases in which non-linearity may exist in a ground-water model. The question to be addressed by the modeler is whether these non-linearities significantly affect the results of the model for the range of stresses of interest. If the non-linearities are negligible, then response functions may be used to approximately describe the response of the system in a general sense. The developer, however, must caution subsequent users of the functions relative to the approximate nature of the functions and the range over which their use is approximately valid.
GENERATING
RESPONSE FUNCTIONS USING MODFLOW
MODFLOW can be used in
either of two ways to generate response functions. It may be either 1) applied
to a single stress with no initial hydraulic gradient, or 2) the user may use
the version MODRSP (Maddock and Lacher, 1991) to directly calculate response
coefficients. Both methods require the same assumptions and produce equivalent
results. Application of MODRSP is normally more convenient than performing multiple
MODFLOW simulations; however, MODRSP currently does not include the Drain Package
and some of the more recently added modules to MODFLOW and does not include
a pre- or post-processor. If newer modules are required for an application,
the most efficient procedure may be to conduct multiple MODFLOW simulations.
A calibrated MODFLOW model of an area can be used, with some modification, to directly calculate response functions. Input adaptations are required to remove all recharge and discharge and eliminate all hydraulic gradients within the system. This procedure was outlined and applied by Hubbell et al (1997) and includes the following steps.
The modified model is run with the single specified stress. System response can be extracted from the model output in either a steady-state or transient form. Development of transient response functions requires that the model include storage characteristics. Response, in terms of changes in aquifer water level, or changes in flux with head-dependent boundaries, can be determined for any desired location by extracting drawdown or flux for that location. In the case of Hubbell et al (1997) the river flux was summed for four reaches of the river and the collective response was described for each river reach. Response to stress at other locations requires repeating the simulation process, again with a single stress used at the point of interest. Hubbell, et al (1997) ran 18 simulations to develop responses for stress at 18 different locations.
An arbitrarily large stress may be used to evaluate the system response. In this case, the stress should be sufficiently large to maintain a reasonably accurate mass balance, minimizing the significance of numerical error. If an arbitrarily large stress is used, the response must be divided by the magnitude of the stress in order to express the results as a response to a unit stress. These results are then easily applied to stresses of any magnitude.
Alternately, a unit stress may be applied at the point of interest. In this case, the iteration closure criteria must be greatly reduced to maintain a valid mass balance and minimize effects of numerical error. The simulated response, however, is produced in a form that is already normalized.
It is also possible to determine the response function as the difference between two simulations where recharge, discharge and hydraulic gradients have not been removed. In this case, the system response at the locations of interest can be expressed as the difference between a simulation with a given stress present and one with the stress absent. The magnitude of the stress, and the closure criteria must be adjusted with consideration of the discussion in the two previous paragraphs.
The second means of obtaining response functions is through application of a MODFLOW variation, MODRSP (Maddock and Lacher, 1991). MODRSP is capable of determining drawdown, velocity, storage loss, and capture response functions. Capture may be stream depletion, change in evapotranspiration, change in head-dependent boundary flux, or leakage from adjacent aquifers. MODRSP is a revision of the 1983 version of the MODFLOW code. Because this program is based on an early version of the program, not all of the currently available packages are accommodated. The SIP, SSOR, and PCG solution packages can be used; however, more recent additions like the Stream-Flow Routing Package are not available. The Drain Package is not included in MODRSP, presumably due to the potential for non-linear effects.
MODRSP solves the finite difference equations for a unit stress for a specified location and duration. Because a unit stress is always used, head change at any location represents the drawdown response function. Capture and storage response functions are calculated from the drawdown response function in the same way as MODFLOW would calculate head-dependent flux or storage change. The velocity response is calculated from inter-cell flow and the equation relating velocity to flow and cell dimensions.
Transient simulations with MODRSP automatically apply a unit stress during the first model stress period. Response functions are provided at the end of each stress period. Response functions generated for subsequent stress periods (after the first) represent the residual effects of the stress through time. Effects of extended pumping may be determined by superimposing response functions with an appropriate time lag.
MODRSP simulates response of the aquifer to a series of stresses at prescribed locations. These stresses are applied through the WELL Package. The user specifies stress locations and MODRSP sequentially simulates individual response to a unit stress at each of the prescribed locations. No other stresses, in the Well Package, Recharge Package, or other packages are input or used. MODRSP automatically applies the previously discussed conditions of no initial hydraulic gradient and no recharge and discharge except at points from which response functions will be evaluated. A personal computer version of MODRSP has been developed in the Civil Engineering Department at Colorado State University.
Either of the two methods described will yield identical response functions. The method chosen should depend on the efficiency of either method for the given situation and the MODFLOW features needed.
ANTICIPATED
APPLICATION OF RESPONSE FUNCTIONS IN THE EASTERN SNAKE RIVER PLAIN
The State of Idaho has
recently committed to conjunctive management of surface and ground water through
the promulgation of conjunctive management rules. These rules focus on the eastern
Snake River Plain that contains most of the surface and ground water irrigation
in the state. The highly productive Snake River Plain aquifer underlies the
eastern Snake River Plain and discharges over 18 million cubic meters per day
in the Thousand Springs and American Falls reaches of the Snake River. These
spring discharges are highly appropriated for irrigation, hydropower, and other
uses. Ground water pumping for irrigation generally has junior water rights
priorities relative to the more senior surface water uses. Ground water users
are, therefore, likely to be held accountable for depletion of spring discharges
and flows of the Snake River.
Although the conjunctive management rules indicate that junior ground water users can be held accountable for depletion of surface water flows, they do not specify a) the rate of accountability, b) how accountability changes with location in the basin, or c) how accountability changes with time. These important details have not yet been determined.
Development of response functions describing cause and effect relationships for different areas of the aquifer and different river reaches may provide a means of understanding and quantifying pumping and recharge impacts on the river. Steady state response functions can be used to identify areas in which pumping most significantly impacts springs along a given reach of the river. Transient response functions will describe the temporal response of spring discharges to ground water pumping or recharge in any given area. It is expected that response functions will be used in a qualitative sense to assist water managers in understanding cause and effect relationships in the aquifer and river and in a quantitative fashion to estimate impacts and mitigation requirements. The U.S. Bureau of Reclamation will also incorporate the response functions into a surface water model of the Snake River.
CONCLUSION
In some cases, response
functions can serve as a valuable qualitative tool to aid in understanding cause
and effect relationships within an aquifer and as a quantitative tool to express,
in simple form, quantitative and transient impacts of ground water pumping and
recharge. Response functions can be generated from multiple MODFLOW simulations
or more simply from the MODFLOW based MODRSP program. Response functions can
be developed to describe how aquifer water levels, aquifer storage, surface
water depletion, or ground water flow velocities are affected by ground water
pumping or recharge in any prescribed location. The primary constraint on the
development and use of response functions is that all significant components
of the system must be represented by linear equations. In areas where the use
of response functions is valid, they can provide a highly useful tool in a water
managerís toolbox.
ACKNOWLEDGEMENTS
This work is supported
by the U.S. Bureau of Reclamation Snake River Resources Review Project (SR3).
The work is conducted in collaboration with the Idaho Department of Water Resources.
REFERENCES
Ejaz, M.S. and R.C. Peralta, 1995. Maximizing Conjunctive Use of Surface and Ground Water under Surface Water Quality Constraints. Advances in Water Resources, v. 18, no. 2, pp. 67-75.
El-Beshri, M.Z. and J.W. Labadie, 1994. Optimal Conjunctive Use of Surface and Groundwater Resources in Egypt. Proceedings of the VIII IWRA World Congress on Water Resources, Cairo, Egypt, Nov. 1994.
Hubbell, J.M., C.W. Bishop, G.S. Johnson, and J.G. Lucas, 1997. Numerical Ground-Water Flow Modeling of the Snake River Plain Aquifer Using the Superposition Technique. Ground Water, v. 35, no. 1, pp. 59-66.
Illangasekare, Tissa and H.J. Morel-Seytoux, 1982. Stream-Aquifer Influence Coefficients as Tools for Simulation and Management. Water Resources Research, v.18, no. 1, pp168-176.
Johnson, G.S., C.W. Bishop, J.M. Hubbell, J.G. Lucas, 1993. Simulation of Impacts of Snake River Plain Aquifer Water Use on Flow in the Snake River. Idaho Water Resources Research Institute, University of Idaho, Moscow, ID, 56 p.
Labadie, J.W., 1991. Program MODSIM: River Basin Network Flow Model for the Microcomputer. Dept. of Civil Engr., Colorado State University, Ft. Collins, CO.
Maddock, Thomas III, 1972. Algebraic Technological Function from a Simulation Model. Water Resources Research, v. 8, no. 1, pp129-134.
Maddock, Thomas III and L.J. Lacher, 1991. MODRSP, a Program to Calculate Drawdown, Velocity, Storage, and Capture Response Functions for Multi-Aquifer Systems. Dept. of Hydrology and Water Resources, University of Arizona, Tucson, AZ.
McDonald, M.G. and A.W. Harbaugh, 1988. A Modular Three-Dimensional Finite-Difference Ground-Water Flow Model. U.S. Geological Survey Techniques of Water-Resources Investigations, Book 6, Chapter A1.
Morel-Seytoux, H.J. and C.J. Daly, 1975. A Discrete Kernel Generator for Stream Aquifer Studies. Water Resources Research, v. 11, no. 2, pp. 253-260.
Reilly, T.E., O.L. Franke, and G.D. Bennett, 1987. The Principle of Superposition and its Application in Ground-Water Hydraulics. U.S. Geological Survey Techniques of Water-Resources Investigations, Book 3, Chapter B6, 28 p.